Resolviendo el oscilador armónico

Empezar este blog hablando del oscilador armónico podría resultar hasta irónico, si está en todos lados, es porque todo el tiempo lo estamos invocando, y más porque se sabe que muchos sistemas en física experimentan movimientos oscilatorios; desde la evolución de los planetas, los péndulos, entre los más comunes, otros menos comunes pueden ser las oscilaciones de átomos en sólidos cristalinos, el movimiento de electrones, entre muchos más.

Decimos que un movimiento es oscilatorio si este repite su movimiento regularmente en el tiempo a lo largo de una trayectoria, y además, se ha visto hasta el cansancio, ametralladoramente, que cada sistema mecánico en las proximidades de su mínimo de potencial realiza movimiento oscilatorio, no son por nada los memes. Está en todos lados.

Entonces, comencemos con la siguiente ecuación:

$\frac{d^2 x}{dt^2} + \frac{b}{m} \frac{dx}{dt} + \frac{k}{m} x = F(t)$

esta ecuación podría resultar un poco familiar, y no es ninguna sorpresa. Se podría comenzar si partimos del famosísimo sistema de una masa atada a un resorte. Sabemos que tenemos:

$F = -kx$

y entonces:

$ma = -kx \rightarrow a = -\frac{k}{m}x \rightarrow \frac{d^2}{dt^2} = -\frac{k}{m}x$

Y por lo tanto,

$\frac{d^2x}{dt^2} + \frac{k}{m}x = 0$

agregamos un término de fricción que afecta la velocidad del sistema, entonces:

$\frac{d^2x}{dt^2} + \frac{b}{m}\frac{dx}{dt}+ \frac{k}{m}x = 0$

el cual comúnmente llamamos amortiguamiento.

Si además agregamos una fuerza, cualquiera sea su naturaleza, dependiente del tiempo, entonces tenemos:

$\frac{d^2x}{dt^2} + \frac{b}{m}\frac{dx}{dt}+ \frac{k}{m}x = F(t)$

Ahora, yo no quiero meterme demasiado en la parte teórica de cómo resolvemos este tipo de ecuaciones diferenciales de forma analítica, y más porque bueno, cuando agregamos este último término al que se le llama forzante, este proceso puede ponerse un poco turbio. Pero hay demasidas fuentes por ahí.

Lo que haremos será resolverlo de forma numérica, usando Julia.

Primero comencemos pensando en el oscilador armónico simple, nada de amortiguamiento, nada de forzante, nada de nada. Esto ahora puede parecer demasiado, resolver el oscilador armónico numéricamente se puede entender como matar a bazucazos a un mosquito, ahora sí que sale mas caro el caldo que las albóndigas, pero tiene su chiste. Servirá para dejar en claro con un ejemplo simple, aspectos importantes a tomar en cuenta a la hora de resolver ecuaciones diferenciales numéricamente.

Comenzamos importando las paquterías que vamos a usar, DifferentialEquations, como su nombre nos delata, la usaremos para resolver ecuaciones diferenciales, es una paquetería muy interesante, con bastantes métodos y ejemplos en su documentación, vale la pena checar. Además se jacta de ser bastante buena a comparación de otras herramientas disponibles, por ejemplo aquí.

using DifferentialEquations, Plots

Es importante prestar atención a la estructura de las funciones que definiremos, comencemos transcribiendo:

$\frac{d^2x}{dt^2} = - \frac{b}{m}\frac{dx}{dt} - \frac{k}{m}x + F(t)$

function oscilador(du, u, p, t)
    b, k, m, F = p 
    -(k/m) * u - (b/m) * du + F(t) 
end

oscilador (generic function with 1 method)

Para resolverlo, en primer lugar, en su forma más simple, definamos los siguientes parámetros.

b = 0 # Factor de amortiguamiento en 0
m = 1.0 # Masa unitaria
k = 1.0 # Constante del resorte unitaria
F(t) = 0 # Fuerza externa igual a cero por el momento
p = (b, m, k, F) # Definimos una tupla con nuestros parámetros

con esos parámetros, nuestra función oscilador() será unicamente $\frac{d^2x}{dt^2} = - \frac{k}{m}x$.

Ahora, como estamos resolviendo una ecuación diferencial de segundo orden, entonces sabemos que necesitamos dos condiciones iniciales, definamos pues, la posición inicial y la velocidad inicial:

u_inicial = 0.25
du_inicial = 0.0

Finalmente, ya sólo nos falta el span de tiempo en el cual queremos resolver, digamos:

tspan = (0.0, 20.0)

Usemos la siguiente estructura para definir nuestro problema de segundo orden, que se puede consultar aquí:

prob = SecondOrderODEProblem(oscilador, du_inicial, u_inicial, tspan, p)

Si sale lo siguiente, es porque todo va bien. Se ha definido nuestro problema, en nuestro span de tiempo con las condiciones iniciales:

ODEProblem with uType RecursiveArrayTools.ArrayPartition{Float64, Tuple{Float64, Float64}} and tType Float64. In-place: false
timespan: (0.0, 20.0)
u0: (0.0, 0.25)

Para resolver, únicamente hacemos:

solucion = solve(prob)

Ahora imprimamos únicamente los primeros 10 resultados, para no llenar de números esto:

solucion[1:10]

retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 10-element Vector{Float64}:
 0.0
 0.00398406374501992
 0.043824701195219126
 0.17040503555409192
 0.3848691269450288
 0.6652747463983004
 1.02689284444547
 1.4605744133795586
 1.9362192263860547
 2.4374270730621967
u: 10-element Vector{RecursiveArrayTools.ArrayPartition{Float64, Tuple{Float64, Float64}}}:
 (0.0, 0.25)
 (-0.000996013301336101, 0.24999801590713389)
 (-0.010952668555771447, 0.24975996286732172)
 (-0.04239538303651577, 0.24637904025402796)
 (-0.09385946099687895, 0.23171189253544547)
 (-0.15431883265022545, 0.19668679605322734)
 (-0.2139238243543623, 0.12936997385540439)
 (-0.24848292540141162, 0.02749949694191406)
 (-0.2334929667920803, -0.0893365569834332)
 (-0.16184878236130407, -0.19053862042407382)

Entonces, lo que estamos viendo es que nos regresa dos vectores, uno es para cada momento del tiempo en que computó la solución, y el otro vector, contiene vectores de dos entradas, la velocidad y la posición respectivamente.

Grafiquemos la solución, haciendo únicamente:

plot(solucion,
linewidth = 2,
title = "Oscilador armónico",
xaxis = "Tiempo (s)",
yaxis = "Velocidad | Posición",
labels = ["Velocidad" "Posición"],
dpi=300
)

Donde obtenemos:

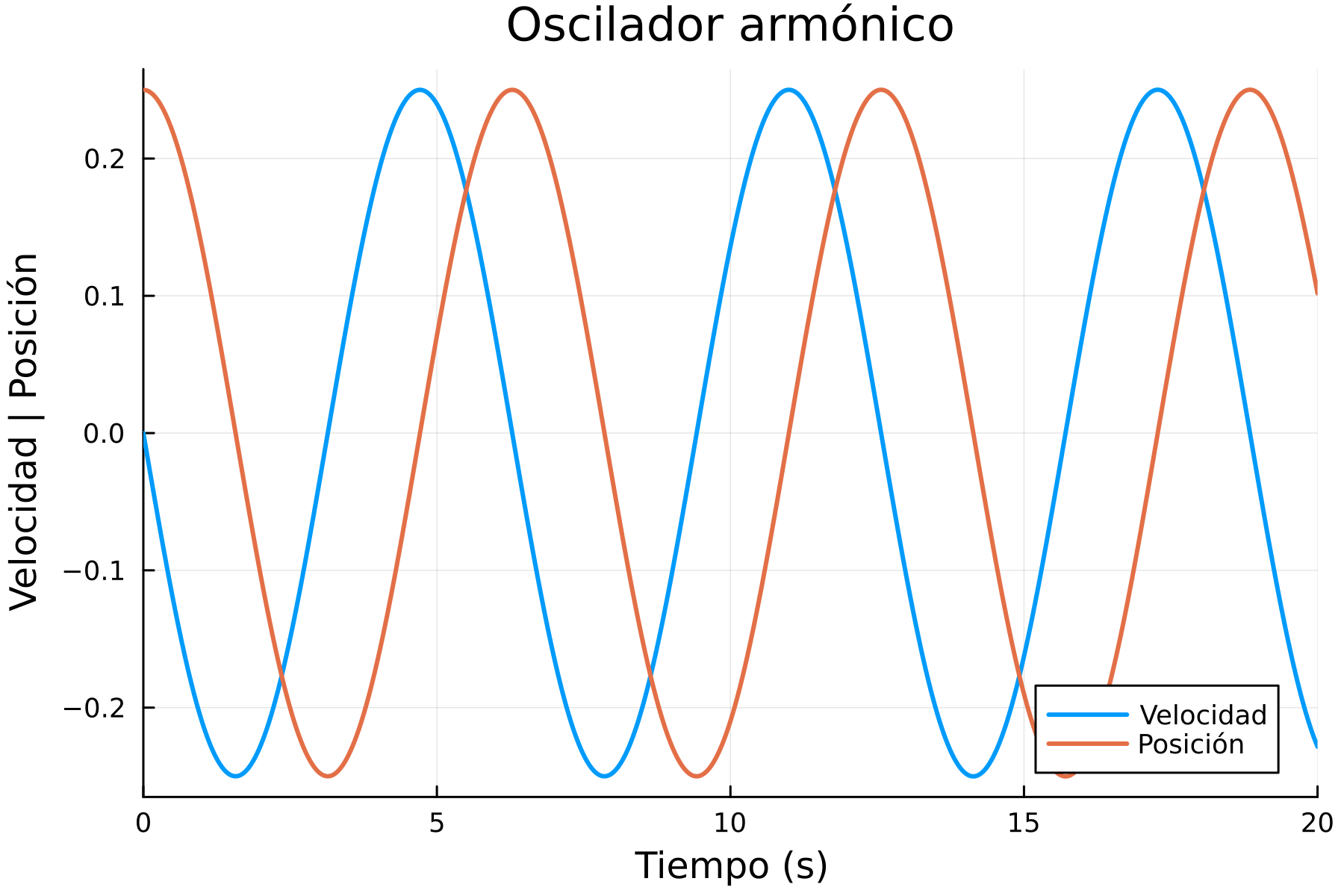
Lo que observamos no es nada que no sabíamos con anterioridad, que la solución del oscilador armónico es $x(t) = A \cos(\omega t + \phi)$ o de la misma forma, $x(t) = A \cos(\omega t) + B \sin(\omega t)$, donde $\omega = \sqrt{\frac{k}{m}}$.

Pero entonces, enfocándonos en la parte numérica de todo esto, nos pueden surgir muchas dudas, pareció magia, simplemente se sintió como apretar un botón, pero no nos enteramos de nada, ni del algoritmo, ni del tamaño del paso, ni de la tolerancia, ni de nada de lo que vemos comúnmente cuando estudiamos métodos numéricos.

Vayamos paso por paso, entendiendo que está pasando. En primer lugar, una pregunta natural que nos podemos hacer después de resolver algo numéricamente, es qué tan cierta es nuestra solución, aquí podríamos hacer como comúnmente se hace, traernos la solución analítica y ver el error que tenemos, pero probemos otro enfoque.

Una de las cosas que tenemos bien claras acerca del oscilador armónico es que este conserva su energía.

Entonces, nuestros resultados nos tienen que mostrar que la energía se conserve. Comencemos obteniendo los valores de velocidad. Como habíamos mencionado, la velociad son los resultados de la primer entrada del vector u, y la posición la segunda entrada, entonces:

velocidad = solucion[1,:]
posicion = solucion[2,:]

Y sabemos que: $E = T + U = \frac{1}{2} m v^2 + \frac{1}{2} k x^2$

cinetica = m .* (velocidad.^2 ./ 2) # El (.) en las operaciones en Julia significa que haremos la operación para cada entrada del vector
potencial = k .* (posicion.^2 ./ 2)
energia = cinetica + potencial

Para obtener las estampas de tiempo de cada resultado, hacemos:

tiempo = solucion.t

Y entonces ahora sí, veamos qué está pasando con la energía:

plot(tiempo, energia,
linewidth = 2,
title = "Energía del scilador armónico",
xaxis = "Tiempo (s)",
yaxis = "Energía",
label = false,
dpi=300
)

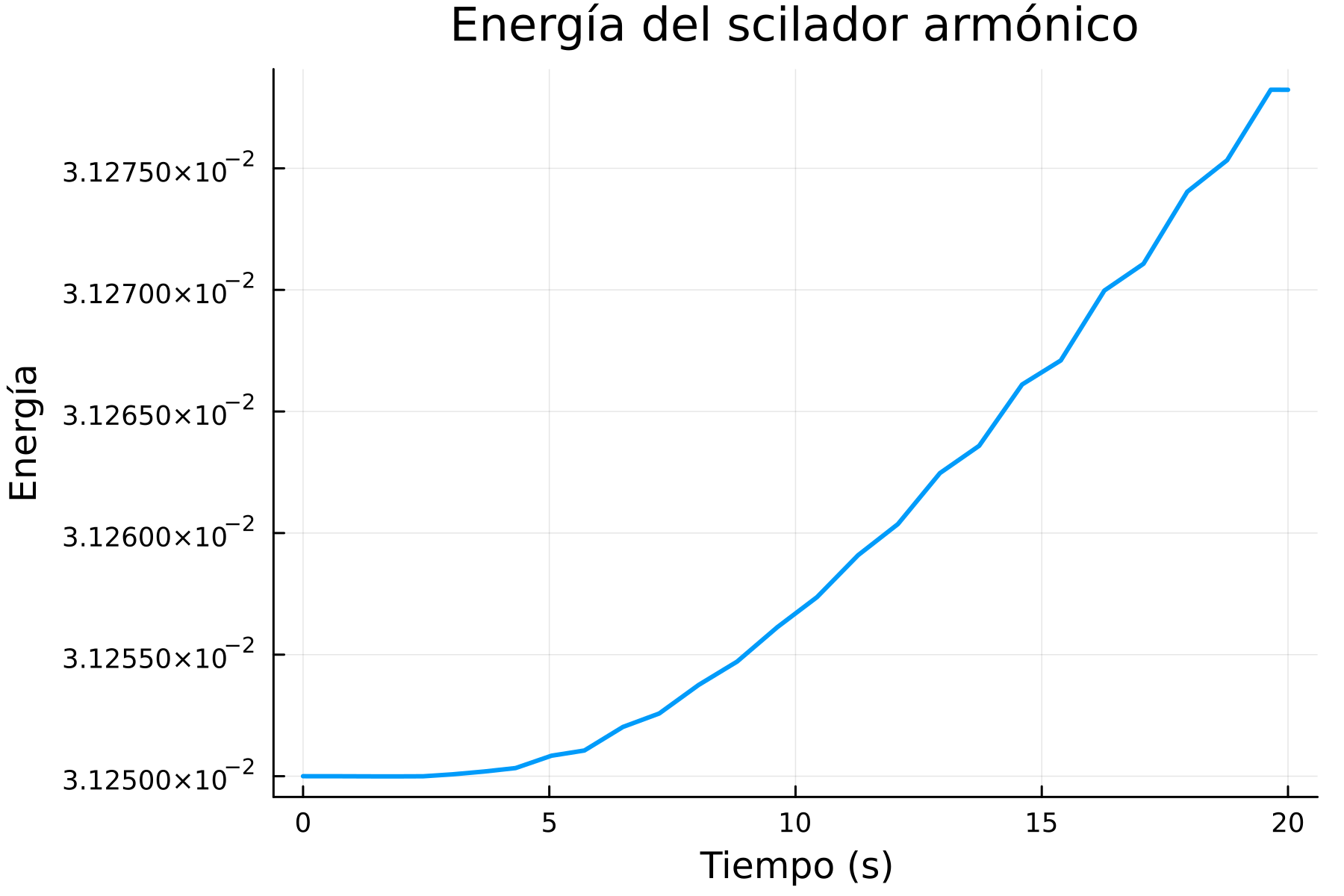
Como podemos ver, aunque tal vez poco, la energía no se está conservando, de hecho, está aumentando, esto no tendría que pasar con el oscilador armónico simple. Ahí está, la culminación de miles de años de ingenio humano se ve reflejado en que la computadora no puede lograr conservar la energía de un simple oscilador. Fin.

Alto ahí, qué tal si hacemos lo siguiente, aunque ya tenemos una gráfica de posición vs tiempo allá arriba, veamos qué pasa si graficamos la posición que obtuvimos de seleccionar la segunda entrada de nuestros resultados, y el tiempo que obtuvimos haciendo solucion.t.

plot(tiempo, posicion,
linewidth = 2,
title = "x vs t",
xaxis = "Tiempo (s)",
yaxis = "Posición",
label = false,
dpi=300
)

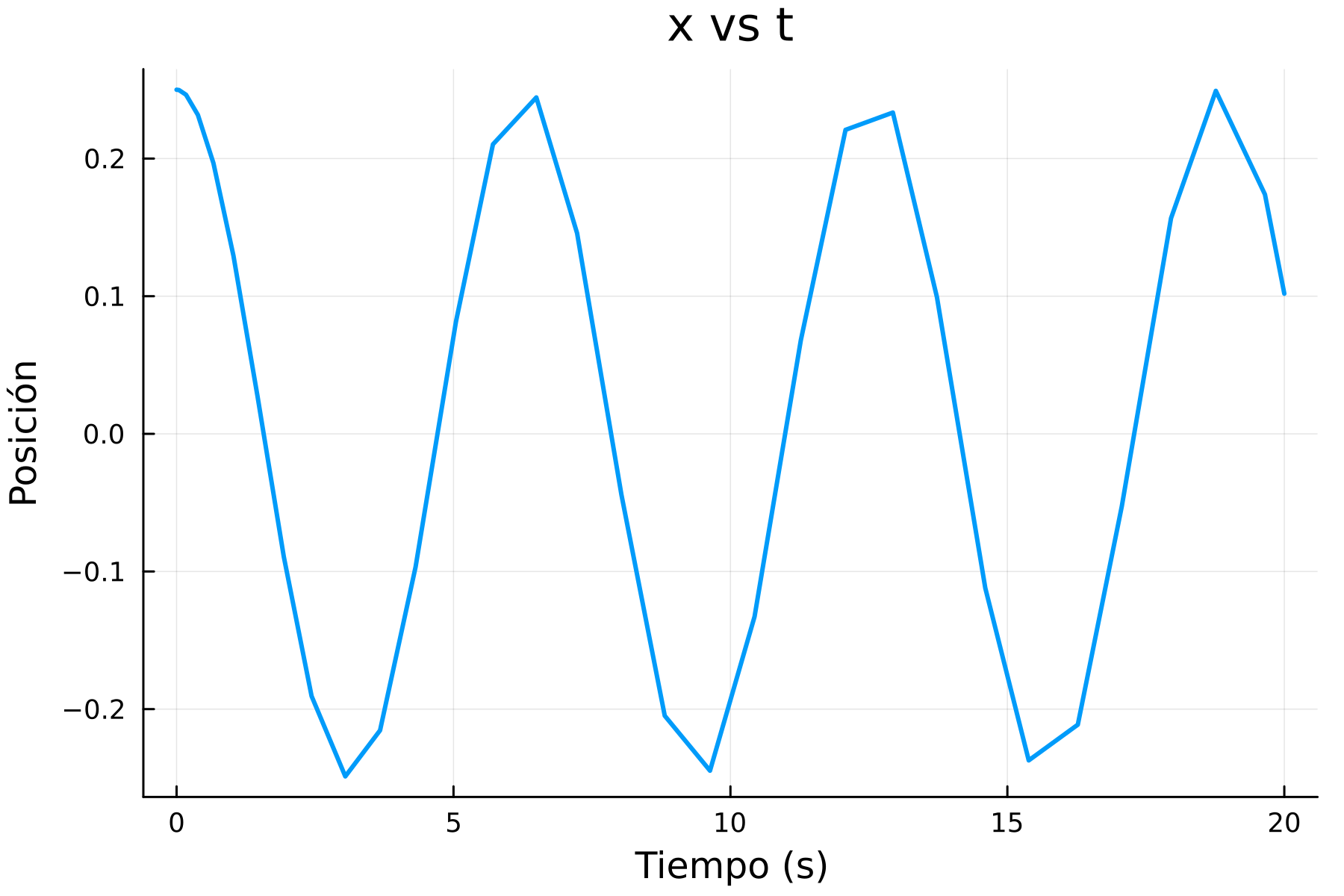
Esto definitivamente no se ve como la gráfica que habíamos obtenido anteriormente, pero si anteriormente hicimos graficar(solucion) y ahora hicimos graficar(tiempo de la solucion, posicion de la solucion), y los resultados se ven bastante diferentes, ¿qué está pasando entonces?

A ver, lo primero que hay que tener en mente es que cuando resolvemos ecuaciones diferenciales de forma numérica, estamos aproximándonos a la solución real de forma discreta, por lo tanto habrá un error en cada paso del cálculo, ya sea porque sabemos que las computadoras no la arman chido con los números flotantes, por la forma en que se implementó el algoritmo, entre muchas cosas más. Algo que podemos hacer es, entonces, jugar con los argumentos que le damos a nuestra función. Aquí podemos encontrar la enorme cantidad de argumentos que podemos especificar para resolver nuestro problema, pero para enfocarnos en uno, en uno fácil, pensemos en la tolerancia del error, modifiquemos la tolerancia absoluta y la tolerancia relativa, volvámonos locos y pongámosla muy pequeña.

solucion_tolerancias = solve(prob, abstol = 1e-15, reltol = 1e-15)
solucion_tolerancias[1:10]

retcode: Success
Interpolation: specialized 7th order lazy interpolation
t: 10-element Vector{Float64}:
 0.0
 0.004774625181200294
 0.01236360800894473
 0.02493410021265082
 0.04280227789377106
 0.06072798286906811
 0.08165962400442964
 0.10394243277055
 0.1280334897059047
 0.15332790491508264
u: 10-element Vector{RecursiveArrayTools.ArrayPartition{Float64, Tuple{Float64, Float64}}}:
 (0.0, 0.25)
 (-0.0011936517599990732, 0.24999715037471099)
 (-0.003090823257574651, 0.2499808928930178)
 (-0.0062328791664356745, 0.24992229035701602)
 (-0.010697302469767168, 0.24977103058575534)
 (-0.015172665854748503, 0.2495391556667213)
 (-0.02039222479815355, 0.24916692631202397)
 (-0.02593884191748481, 0.24865071180268064)
 (-0.03192099413679099, 0.24795372579035582)
 (-0.038181958755190044, 0.24706707191695332)

Ahora graficamos:

plot(solucion_tolerancias.t, solucion_tolerancias[2,:],
linewidth = 2,
title = "x vs t",
xaxis = "Tiempo (s)",
yaxis = "Posición",
label = false,
dpi=300
)

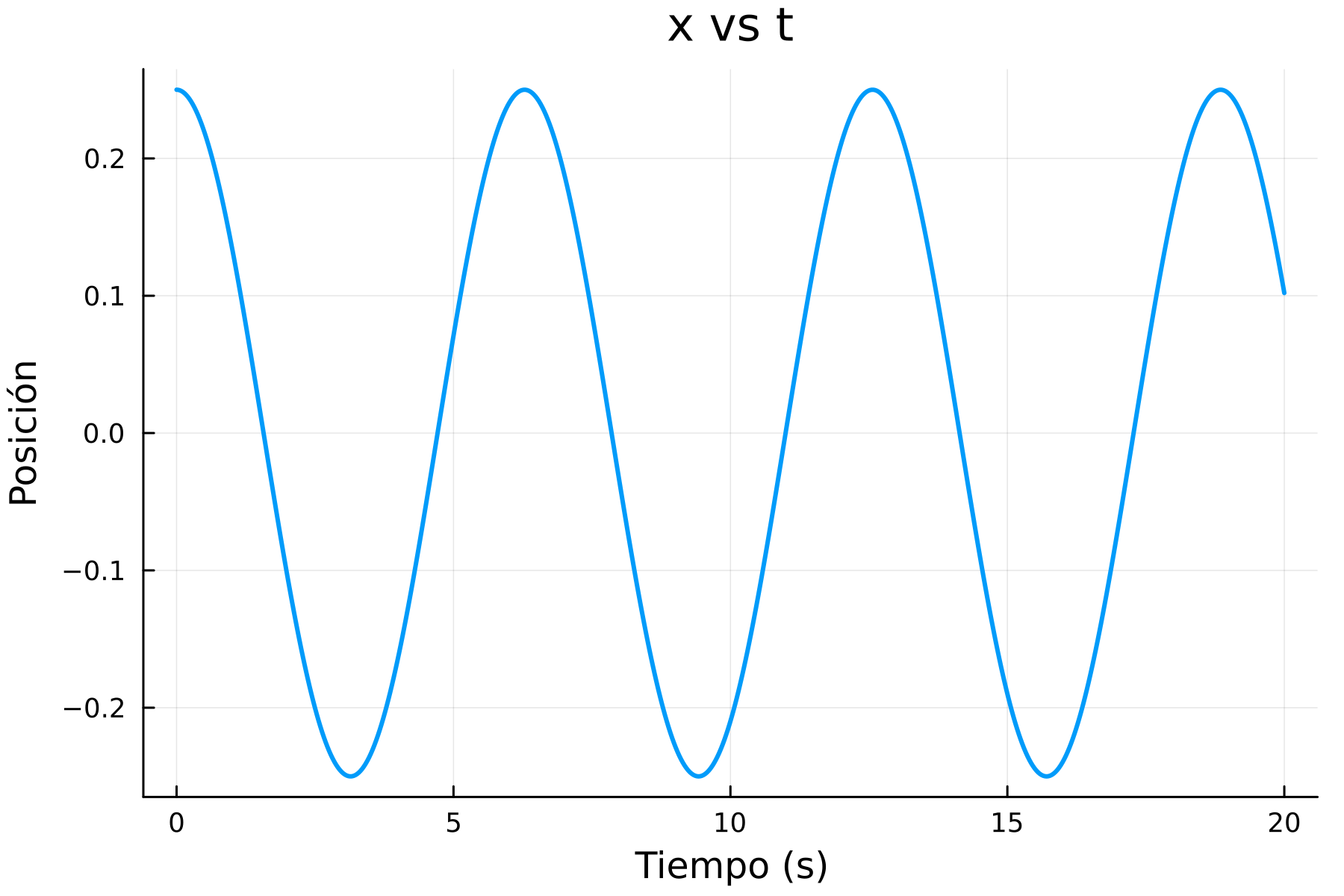
Como podemos ver, mejoró demasiado, pero ahora veamos qué tal con la energía, repetimos nuestros pasos para calcular la energía, graficamos y obtenemos:

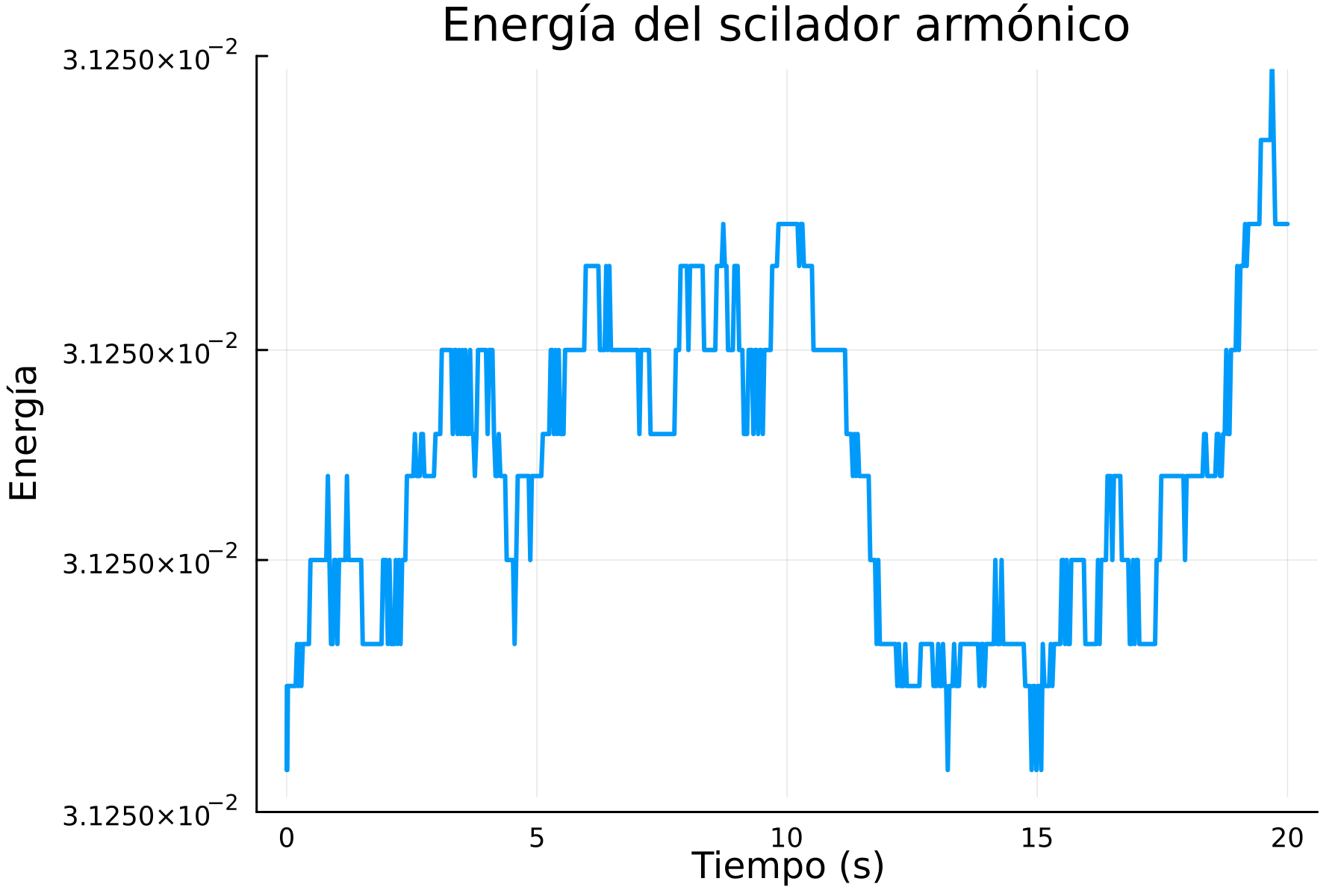
Bueno, parece que mejoró un poco, al menos pareciera que la energía ya no está aumentando tanto, aún existen pequeños problemas, así que aquí entra otra cuestión importante a la hora de resolver problemas de esta manera y con el manejo de las soluciones que obtenemos usando esta paquetería.

Primero observemos lo siguiente, veamos cuántos datos estábamos graficando en el primer ejemplo todo feo:

length(solucion)

33

Con razón, son tan pocos resultados, y si vemos cuantos cuando cambiamos la tolerancia, obtenemos:

length(solucion_tolerancias)

639

Bastante más, entonces tiene sentido que nuestras gŕaficas se vean mejor, además de que estamos disminyendo la toleancia del error, que de por sí eso ya es un costo computacional más alto, estamos simplemente graficando más datos.

PERO, ¿entonces por qué cuando hicimos únicamente plot(solucion) se veía infinitamente mejor, ¿qué no eran únicamente 33 resultados?, ¿para empezar por qué unicamente 33 resultados?, ¿no son demasiado pocos?, ¿qué está pasando?

Bueno, en primer lugar hay que aclarar lo de los resultados, por qué es que nos está regresando tan pocos resultados, la respuesta es que esto no es del todo cierto. Lo que es cierto es que el solucionador, es decir, al hacer solve(prob), nos regresa una solución continua, eso hay que tenerlo claro. Los pocos resultados que estamos viendo son en los puntos tal que el solucionador en efectó computó el problema. Sin embargo, el solucionador incluye una función de interpolación que aproxima la solución para cualquier tiempo dado. Rápidamente podemos recordar a la interpolación como un método para construir nuevos puntos de datos dentro de un conjunto discreto de puntos conocidos.

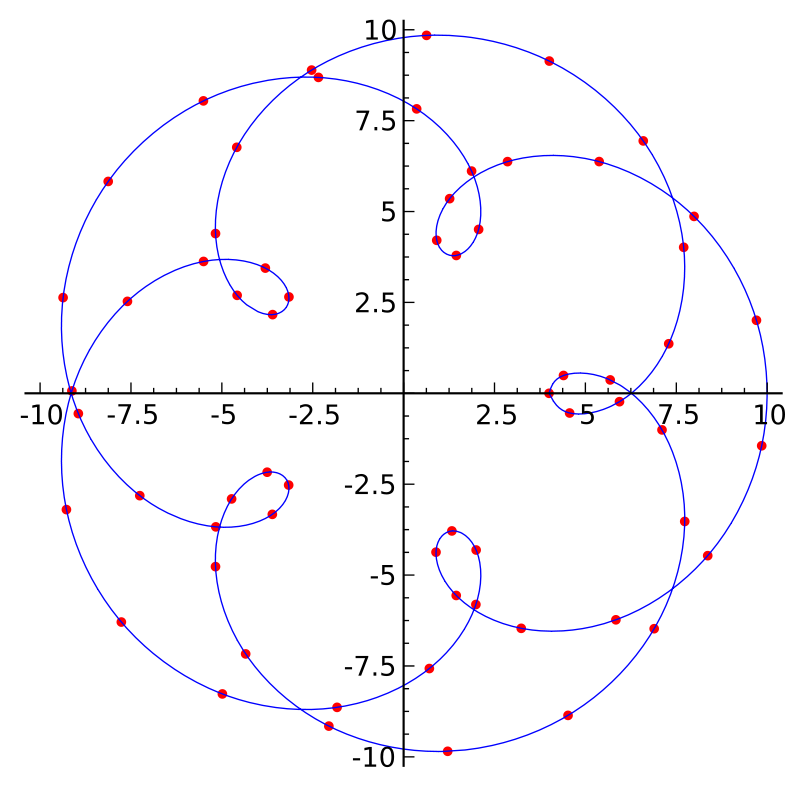
Ahora, para dejar en claro que el solucinador en realiad nos regresa una solución continua podríamos evaluar la solución en algunos puntos en específico.

Podemos generar una serie de puntos, digamos que también dentro de neustro span de tiempo, pero que sean 1000 puntos.

T = range(0,20,length=1000)

0.0:0.02002002002002002:20.0

Y entonces evaluar esos puntos en nuestra solución:

solucion_1000 = solucion(T)
length(solucion_1000)

1000

Como podemos ver, en efecto nos regresa 1000 resultados, podemos evaluarla en diez mil, en cincuenta mil, en un millón, pero bueno ahí ya cada quién sus deseos. El chiste es que la solución es continua.

Ahora sí, regresando a nuestro problema que estamos teniendo con la energía. Hay que tener en claro que resolver numéricamente ecuaciones diferenciales es más que simplemente presionar el botón resolver. Hay una gran cantidad de factores a considerar, como ya vimos, la tolerancia, el tamaño del paso, la rigidez del problema y muchos más.

La clave está en comprender los algoritmos que estamos utilizando. No todas las ecuaciones son iguales y, de manera similar, no todos los métodos numéricos son universalmente aplicables. Cada algoritmo tiene sus propias fortalezas y debilidades. Por ejemplo, en problemas donde la conservación de la enrgía es primordia, los algoritmos simplécticos brillan.

Para empezar ¿qué es simpléctico? Sí, mira te cuento, simpléctico quiere decir que la solución existe en una variedad simpléctica, y bueno según Wikipedia, ...En geometría diferencial, una rama de las matemáticas, una variedad simpléctica es una variedad suave, M, equipada con una 2-forma diferencial cerrada y no degenerada $\omega$, llamada la forma simpléctica. El estudio de las variedades simplécticas se llama geometría simpléctica o topología simpléctica... y bla, bla, bla, bla...

Hay muchas formas y recursos para estudiar este tema, es muy amplio, denso y hasta bonito, pero sin duda, para eso hay quienes lo expliquen infinitamente mejor de lo que yo podría, aquí una de mis publicaciones favoritas acerca de eso.

Entonces, vamos a buscar algún algoritmo simpléctico en la documentación de la paquetería.

Aquí usaremos el algoritmo KahanLi8(), y para esto nos pide ajustar el paso, entonces hagamos:

solucion_simplectica = solve(prob, KahanLi8(), dt=1/10)
solucion_simplectica[1:10]

retcode: Success
Interpolation: 3rd order Hermite
t: 10-element Vector{Float64}:
 0.0
 0.1
 0.2
 0.30000000000000004
 0.4
 0.5
 0.6
 0.7
 0.7999999999999999
 0.8999999999999999
u: 10-element Vector{RecursiveArrayTools.ArrayPartition{Float64, Tuple{Float64, Float64}}}:
 (0.0, 0.25)
 (-0.02495835416170718, 0.24875104131950634)
 (-0.049667332698765575, 0.2450166444603102)
 (-0.07388005166533528, 0.2388341222814012)
 (-0.0973545855771631, 0.23026524850072075)
 (-0.1198563846510513, 0.2193956404725924)
 (-0.14116061834875943, 0.20633390372741853)
 (-0.16105442180942334, 0.19121054682112074)
 (-0.1793390227248812, 0.1741766773367896)
 (-0.19583172740687121, 0.15540249206766393)

Ahora hacemos los mismos pasos para graficar la energía, y ahora observamos:

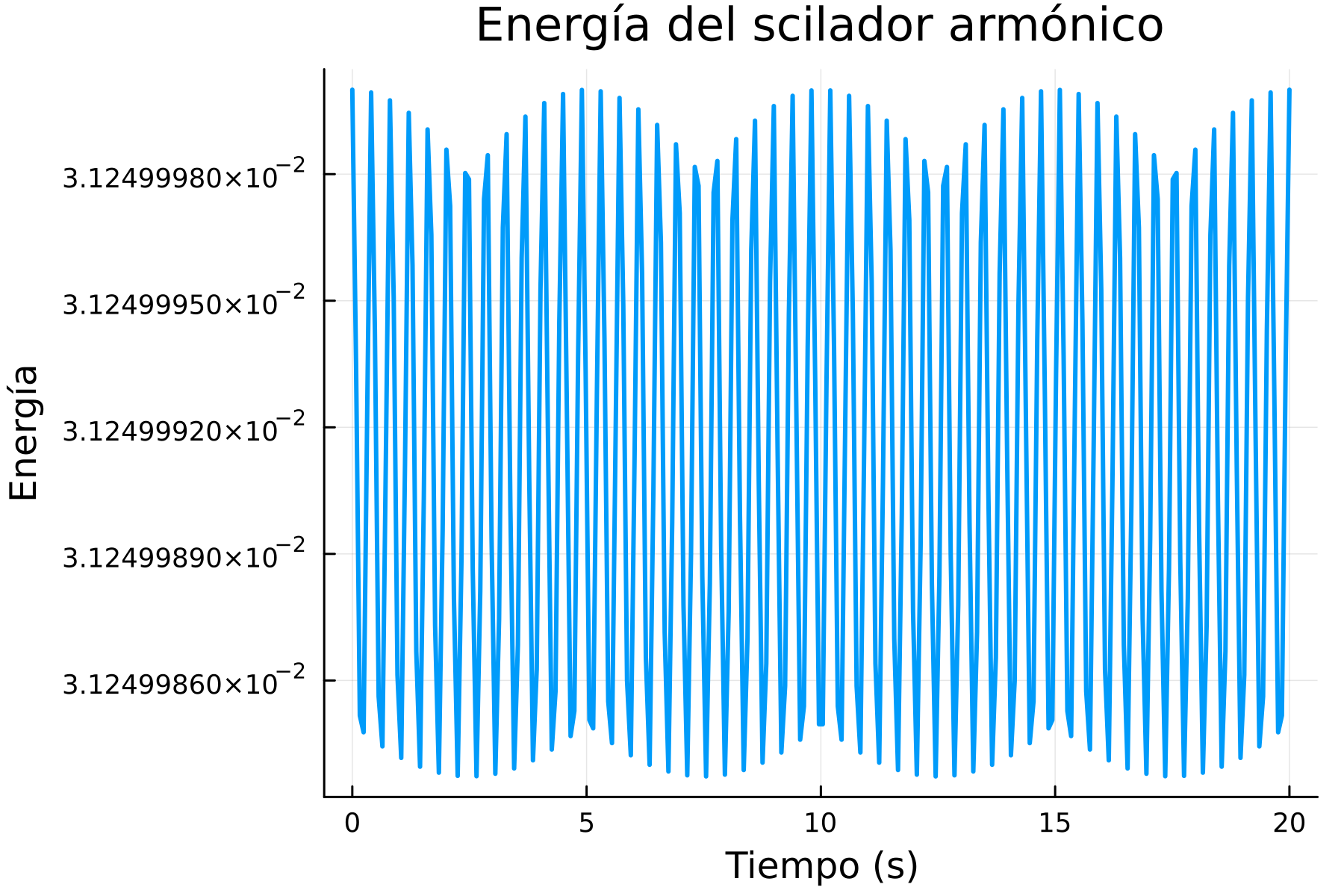
Se ve mejor, porque en esencia ya no observamos esa especie de drift que se observaba en los casos anteriores, y lo que vemos ahora es que la energía está oscilando entre su valor real.

Para continuar, podemos resolver rápidamente el oscilador amortiguado, es decir, modificaremos el parámetro b de nuestra ecuación, para esto sabemos que podemos tener tres escenarios: sub-amortiguamiento, sobre-amortiguamiento y un amortiguamiento crítico.

Cada estado está caracterizado por la relación que existe entre los parámetros de amortiguamiento y la constante del resorte, por ejemplo, ahora nos encontramos en este caso:

$\frac{d^2x}{dt^2} + \frac{b}{m}\frac{dx}{dt}+ \frac{k}{m}x = 0$

Entonces definamos lo siguiente para mayor claridad: $\beta = \frac{b}{2m}$ y $\Omega^2 = \frac{k}{m}$.

Así, entonces tenemos:

$\frac{d^2x}{dt^2} + 2 \beta\frac{dx}{dt}+ \Omega^2 x = 0$

Para que de esta forma sea un poco más cómodo trabajar con la ecuación si lo quiesiéramos hacer analíticamente, pues sabemos que tendríamos que buscar una solución de la forma $x = \exp{\lambda t}$ tal que $\lambda$ satisfaga:

$\lambda^2 + 2 \beta \lambda + \Omega^2 = 0$

y entonces tendríamos:

$(\lambda + \beta)^2 = \beta^2 - \Omega^2$

donde justamente salen a la luz los tres casos anteriores que teníamos:

• Sub-amortiguamiento cuando $\beta < \Omega$

• Sobre-amortiguamiendo cuando $\beta > \Omega$

• Amortiguamiento crítico cuando $\beta = \Omega$

Aquí me ocuparé únicamente del caso $\beta < \Omega$, ya que, a mi criterio, considero el más interesante y los demás serían análogos.

Para este caso, se puede llegar analíticamente a que: $x = e^{-\beta t} = (A \cos{\Omega_{D}t} + B \sin{\Omega_{D}t})$, donde $\Omega_D = (\Omega^2 - \beta^2)^{\frac{1}{2}}$.

Lo interesante de este resultado, como vamos a observar, es que la solución sigue exhibiendo oscilaciones, pues vemos senos y vemos cosenos, pero lo que también vemos es una exponencial negativa, y bueno, una exponencial negativa no perdona. Teóricamente el resultado nos dice que habrá oscilaciones infinitas aún, pero que decaerán exponencialmente. Entonces veamos:

Démosle un nuevo valor a b, tal que se cumpla la condición de sub-amortiguamiento.

b = 0.35
p = (b, m, k, F)

Y reutilicemos todo, exceto claro, nuestros parámetros que es lo que cambiamos.

prob_amortiguado = SecondOrderODEProblem(oscilador, du_inicial, u_inicial, tspan, p)

ODEProblem with uType RecursiveArrayTools.ArrayPartition{Float64, Tuple{Float64, Float64}} and tType Float64. In-place: false
timespan: (0.0, 20.0)
u0: (0.0, 0.25)

Ahora resolvamos utilizando un método Runge-Kutta simplementa.

sol_amortiguado = solve(prob_amortiguado, Tsit5())
sol_amortiguado[1:10]

retcode: Success
Interpolation: specialized 4th order "free" interpolation
t: 10-element Vector{Float64}:
 0.0
 0.00398406374501992
 0.043824701195219126
 0.17792304447975538
 0.4094751846634577
 0.7152390795997883
 1.104073360843106
 1.552204239900723
 2.0414571110125554
 2.531056227837695
u: 10-element Vector{RecursiveArrayTools.ArrayPartition{Float64, Tuple{Float64, Float64}}}:
 (0.0, 0.25)
 (-0.0009953191924160644, 0.24999801682903336)
 (-0.010869096857591722, 0.24976118541787234)
 (-0.04289693870616666, 0.24613397267418452)
 (-0.09272946715811699, 0.2302827387273943)
 (-0.14505234293696384, 0.19350011804164607)
 (-0.18528899933555118, 0.1282741267460104)
 (-0.19334389401083232, 0.0419388850731901)
 (-0.1607830046890981, -0.0462258213850113)
 (-0.09862443175652391, -0.11058080226346037)

Graficamos nuestros resultados análogamente a los casos anteriores y obtenemos:

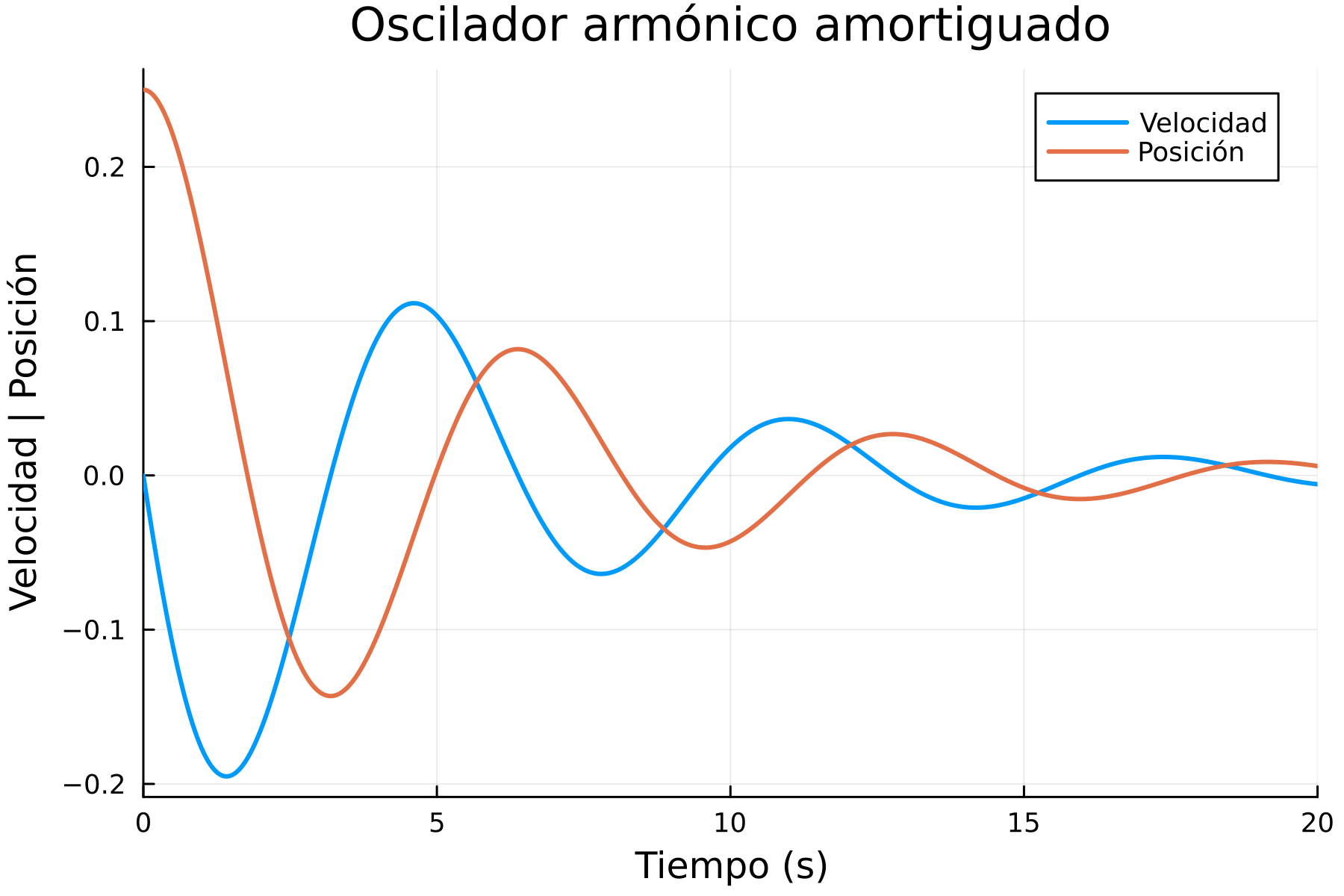
Como se esperaba, un movimiento oscilatorio que se ve opacado por el decaimiento exponencial que lo acompaña.

Ahora, veamos como se haría el último caso, de manera muy similar, ahora definamos una fuerza externa que dependa del tiempo:

F(t) = 2*cos(t)

F (generic function with 1 method)

Entonces, actualicemos nuestros parámetros:

p = (b, m, k, F)

Definimos un nuevo problema con esos parámetros:

prob_am_forzado = SecondOrderODEProblem(oscilador, du_inicial, u_inicial, tspan, p)

ODEProblem with uType RecursiveArrayTools.ArrayPartition{Float64, Tuple{Float64, Float64}} and tType Float64. In-place: false
timespan: (0.0, 20.0)
u0: (0.0, 0.25)

Y lo resolvemos de la misma forma usando el algoritmo por defecto, que no es necesario especificar:

sol_am_forzado = solve(prob_am_forzado, Tsit5())
sol_am_forzado[1:10]

Finalmente, graficamos y obtenemos:

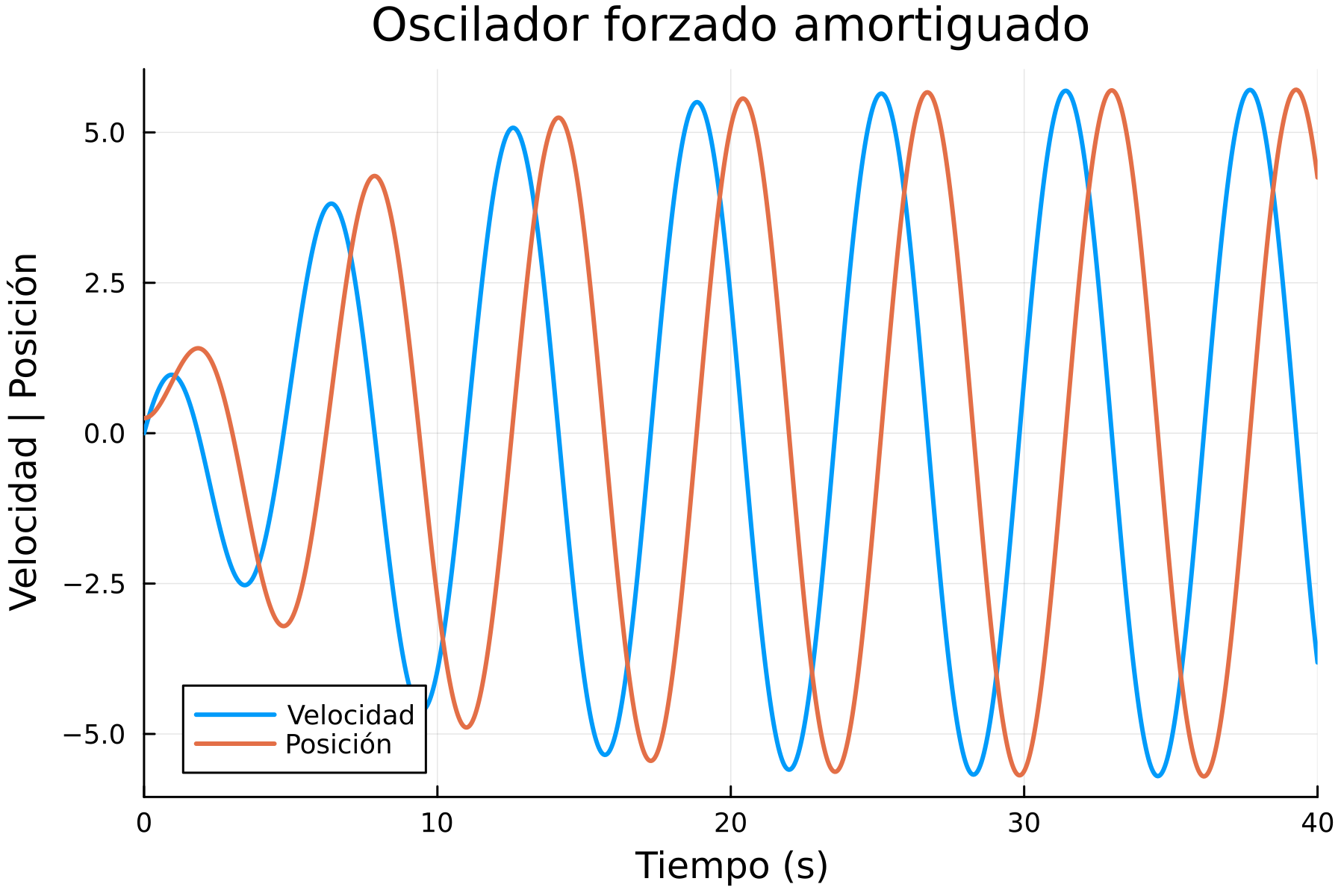
Y como podemos ver, aunque sige habiendo amortiguamiento, la fuerza externa sobresale más. Además, si hemos sido atentos, podemos darnos cuenta que la frecuencia natural del oscilador es la misma que la de la fuerza aplicada, ambos son 1.0. Por lo tanto, como estamos viendo en la gráfica, hay resonancia.