Problema

A veces, al resolver problemas de física, algunas de las cosas que más me han molestado es: una, sufrir por la talacha y dos; no hay dos.

A ver, como físicos, siempre nos vamos a enfrentar a la talacha, a veces es el pan de cada día. No hay manera de terminar con ella, pero sí de hacerla más soportable.

Entonces, lo que haremos hoy, será resolver uno de esos problemas que requeriría un buen arrastre del lápiz, pero sin usar el lápiz.

El problema es el siguiente:

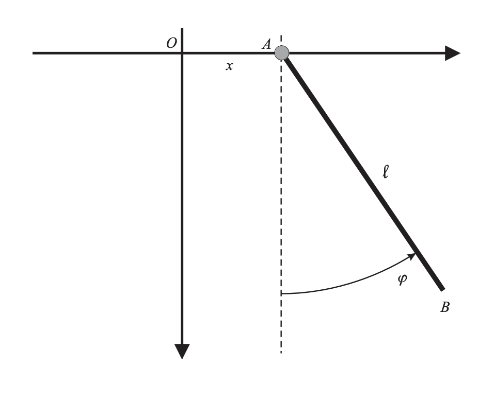
1. El punto A de una barra AB se puede mover sin fricción a lo largo de una línea horizontal (eje x). La barra es homogénea de masa m y longitud l. Se mueve en un plano vertical donde puede rotar libremente alrededor de A. Sobre A se ejerce una fuerza periódica en el eje horizontal $F_x = \frac{1}{3} mg \cos(\Omega t)$, donde $\Omega^2 = \frac{g}{l}$. Encontrar las ecuaciones de movimiento y resolverlas asumiendo que el ángulo $\theta$ y la velocidad angular $\dot{\theta}$ son pequeños. Usar las condiciones iniciales $x(0) = \dot{x}(0) = 0$ y $\theta(0) = \dot{\theta}(0)$.

Lo primero que haremos será importar la primera paquetería que vamos a usar.

Para la talacha usaremos SymPy, esta es una paquetería de Python que estamos llamando desde Julia, la usaremos para los cálculos simbólicos.

using SymPy

Comenzamos definiendo nuestras variables y nuestras funciones. Para entender rápidamente cuáles serán variables y cuáles funciones, primero hay que tener una idea clara de los grados de libertad de nuestro sistema y de las coordenadas canónicas, entonces, observando el sistema podemos concluir que las coordenadas canónicas serán la distancia en $x$ y el ángulo $\theta$ en el cual está rotando la barra.

Como en nuestro problema estamos lidiando con un sólido rígido, entonces nos interesan las coordenadas de su centro de masa: $x_{cm}$ y $y_{cm}$.

$m$ es la masa, $g$ la gravedad, $l$ la longitud de la barra, $t$ el tiempo.

@syms m g y_cm x_cm l t  # Así definimos variables
θ = SymFunction("θ")(t)  # Así definimos funciones
x = SymFunction("x")(t)

Ahora necesitamos definir nuestras derivadas para cada una de nuestras funciones, esto para que nos sean más fáciles algunas operaciones futuras.

xdot = diff(x, t)
xddot = diff(xdot, t)
thetadot = diff(θ, t)
thetaddot = diff(thetadot, t)

Obtenemos las coordenadas del centro de masa de la barra:

x_cm = x + l//2 * sin(θ)

$\frac{l \sin{\left(θ{\left(t \right)} \right)}}{2} + x{\left(t \right)}$

y_cm = l//2*cos(θ)

$\frac{l \cos{\left(θ{\left(t \right)} \right)}}{2}$

Derivamos nuestras variables haciendo:

x_cmd = diff(x_cm, t)

$\frac{l \cos{\left(θ{\left(t \right)} \right)} \frac{d}{d t} θ{\left(t \right)}}{2} + \frac{d}{d t} x{\left(t \right)}$

y_cmd = diff(y_cm, t)

$- \frac{l \sin{\left(θ{\left(t \right)} \right)} \frac{d}{d t} θ{\left(t \right)}}{2}$

El siguiente paso es obtener la energía cinética, al tratar con un sólido rígido, sabemos que la energía cinética es de la siguiente forma: $T = T_{cm} + T_{rotacional}$. Y es aquí en donde empezaría la talacha si tuviéramos que arrastrar el lápiz. Pero hoy no. Comencemos con $T_{cm}$, esta está fácil, sabemos muy bien que $T_{cm} = \frac{1}{2} m ( \dot{x_{cm}}^2 + \dot{y_{cm}}^2 )$, entonces:

T_cm = 1//2 * m * (x_cmd^2 + y_cmd^2)

$\frac{m \left(\frac{l^{2} \sin^{2}{\left(θ{\left(t \right)} \right)} \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{4} + \left(\frac{l \cos{\left(θ{\left(t \right)} \right)} \frac{d}{d t} θ{\left(t \right)}}{2} + \frac{d}{d t} x{\left(t \right)}\right)^{2}\right)}{2}$

Como podemos ver, aún no está tan bien, personas inteligentes como nosotros hubieramos usado la identidad $\sin^2 x + \cos^2 x = 1$

Eso no es problema, podemos hacer simplemente:

T_cm = simplify(expand(T_cm))

$\frac{m \left(l^{2} \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2} + 4 l \cos{\left(θ{\left(t \right)} \right)} \frac{d}{d t} x{\left(t \right)} \frac{d}{d t} θ{\left(t \right)} + 4 \left(\frac{d}{d t} x{\left(t \right)}\right)^{2}\right)}{8}$

Y damos gracias no haber hecho esa talachita.

Nuestro siguiente paso es obtener la energía cinética rotacional. Para esta sabemos que $T_{rot} = \frac{1}{2} \omega I_{cm} \omega$, aquí estamos suponiento que $I_{cm}$ es el tensor de inercia para ejes en el cuerpo respecto al centro de masa, este tensor, si es que la vida no nos odia demasiado aún, la mayoría de las veces es dado en problemas de este tipo. Continuando, $\omega$ es la velocidad angular, nuestro cuerpo rota respecto al ángulo $\theta$, por lo tanto, con la regla de la mano derecha tendríamos: $\omega = \dot{\theta} \hat{z}$.

I = sympy.diag(0, m*l^2 // 12, m*l^2 // 12)

$\begin{bmatrix} 0 & 0 & 0 \\ 0 & \frac{l^2 m}{12} & 0 \\ 0 & 0 & \frac{l^2 m}{12} \end{bmatrix}$

ω = Matrix([0 0 diff(θ, t)])

$\omega = \begin{bmatrix} 0 & 0 & \frac{d\theta}{dt} \end{bmatrix}$

T_rot = (1//2)*ω*I*ω.T # .T para trasponer la matriz y poder hacer la operación

T_rot = T_rot[1]

$\frac{l^{2} m \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{24}$

Finalmente, sumamos nuestras dos energías cinéticas y obtenemos la energía cinética total.

T = T_cm + T_rot

$\frac{l^{2} m \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{24} + \frac{m \left(l^{2} \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2} + 4 l \cos{\left(θ{\left(t \right)} \right)} \frac{d}{d t} x{\left(t \right)} \frac{d}{d t} θ{\left(t \right)} + 4 \left(\frac{d}{d t} x{\left(t \right)}\right)^{2}\right)}{8}$

La expandimos, para que no se vea tan grosera.

T = expand(T)

$\frac{l^{2} m \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{6} + \frac{l m \cos{\left(θ{\left(t \right)} \right)} \frac{d}{d t} x{\left(t \right)} \frac{d}{d t} θ{\left(t \right)}}{2} + \frac{m \left(\frac{d}{d t} x{\left(t \right)}\right)^{2}}{2}$

Ahora definimos una nueva variable, $\Omega$, que es la frecuencia de la fuerza que se aplica en el eje x.

@syms Ω

Para obtener la energía potencial, tenemos que sumar la que es debido a la gravedad, y el potencial asociado a la fuerza. Lo obtenemos recordando que: $U(\mathbf{x}) = -\int \mathbf{F}(\mathbf{x}) \cdot d\mathbf{x}$

Por lo tanto:

U = -(m*g*l//2)*cos(θ) - integrate(1//3 * m*g*cos(Ω*t), x)
U = simplify(U)

$- \frac{g m \left(3 l \cos{\left(θ{\left(t \right)} \right)} + 2 x{\left(t \right)} \cos{\left(t Ω \right)}\right)}{6}$

Finalmente ya tenemos todo para obtener el Lagrangiano, entonces:

L = T - U

$\frac{g m \left(3 l \cos{\left(θ{\left(t \right)} \right)} + 2 x{\left(t \right)} \cos{\left(t Ω \right)}\right)}{6} + \frac{l^{2} m \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{6} + \frac{l m \cos{\left(θ{\left(t \right)} \right)} \frac{d}{d t} x{\left(t \right)} \frac{d}{d t} θ{\left(t \right)}}{2} + \frac{m \left(\frac{d}{d t} x{\left(t \right)}\right)^{2}}{2}$

Obtenemos las ecuaciones de Euler - Lagrange, tal que: $\frac{d}{dt} \left( \frac{\partial L}{\partial \dot{q}_i} \right) - \frac{\partial L}{\partial q_i} = 0$

Para $x$:

ELX = diff(diff(L, xdot), t) - diff(L, x)

$- \frac{g m \cos{\left(t Ω \right)}}{3} - \frac{l m \sin{\left(θ{\left(t \right)} \right)} \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{2} + \frac{l m \cos{\left(θ{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} θ{\left(t \right)}}{2} + m \frac{d^{2}}{d t^{2}} x{\left(t \right)}$

Para $\theta$:

ELθ = diff(diff(L, thetadot), t) - diff(L, θ)

$\frac{g l m \sin{\left(θ{\left(t \right)} \right)}}{2} + \frac{l^{2} m \frac{d^{2}}{d t^{2}} θ{\left(t \right)}}{3} + \frac{l m \cos{\left(θ{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} x{\left(t \right)}}{2}$

Ahora despejamos para $\frac{d^{2}}{d t^{2}} x$ de la siguiente forma:

sol_1 = solve(ELX, xddot)

sol_1[1]

$\frac{g \cos{\left(t Ω \right)}}{3} + \frac{l \sin{\left(θ{\left(t \right)} \right)} \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{2} - \frac{l \cos{\left(θ{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} θ{\left(t \right)}}{2}$

Y para $\frac{d^{2}}{d t^{2}} θ$ :

sol_2 = solve(ELθ, thetaddot)
sol_2[1]

$- \frac{3 g \sin{\left(θ{\left(t \right)} \right)} + 3 \cos{\left(θ{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} x{\left(t \right)}}{2 l}$

Muy bien, ya tenemos nuestras ecuaciones de movimiento, ahora nos toca resolverlas. El problema nos pide asumir ángulos pequeños, esto porque así nos libraríamos de varios términos feos, porque a veces trabajar analíticamente con las ecuaciones de movimiento que obtenemos no sólo es difícil, puede resultar imposible.

Pero aquí no nos estamos manchando las manos, y además tenemos nuestras poderosas computadoras, entonces resolvamos como dios manda.

Empezamos importando las siguientes paqueterías de Julia:

using DifferentialEquations, Plots

Definimos nuestros parámetros, la gravedad de nuestro planeta, una longitud de 1.0, y la frecuencia definida como el problema nos dice. Además el span de tiempo para el cual queremos resolver la ecuación, en forma de tupla.

params = (9.81, 1.0, sqrt(9.81/1.0))
tspan = (0.0, 10.0)

Recordamos los dos monstruos que acabamos de obtener:

$\frac{d^{2}}{d t^{2}} x = \frac{g \cos{\left(t Ω \right)}}{3} + \frac{l \sin{\left(θ{\left(t \right)} \right)} \left(\frac{d}{d t} θ{\left(t \right)}\right)^{2}}{2} - \frac{l \cos{\left(θ{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} θ{\left(t \right)}}{2}$

y

$\frac{d^{2}}{d t^{2}} θ = - \frac{3 g \sin{\left(θ{\left(t \right)} \right)} + 3 \cos{\left(θ{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} x{\left(t \right)}}{2 l}$

Definimos una función de la siguiente forma en donde únicamente transcribiremos esas ecuaciones a código, hay que ser cuidadosos en respetar la estructura. Tomamos de una vez $l = 1$ para que se vea más limpio el código.

function cuerpo_rigido(ddu, du, u, p, t)
    g, l, Ω = p


    ddu[1] = (g * cos(t * Ω) / 3) + (sin(u[2]) * du[2]^2 / 2) - (cos(u[2]) * ddu[2] / 2)
    ddu[2] = -3/2 * (g * sin(u[2]) + cos(u[2]) * ddu[1]) 
end

cuerpo_rigido (generic function with 1 method)

Definimos nuestras condiciones iniciales, tal cual se nos pide.

u0 = [0.0, 0.0]
du0 = [0.0, 0.0]

Y ahora definimos el problema de la siguiente forma:

prob_CR = SecondOrderODEProblem(cuerpo_rigido, du0, u0, tspan, params)

ODEProblem with uType RecursiveArrayTools.ArrayPartition{Float64, Tuple{Vector{Float64}, Vector{Float64}}} and tType Float64. In-place: true
timespan: (0.0, 10.0)
u0: ([0.0, 0.0], [0.0, 0.0])

Eso significa que todo va bien, que tenemos bien definido nuestro problema con ese span de tiempo, y esas condiciones iniciales.

Ahora, ya se ha discutido aquí, que resolver ecuaciones diferenciales numéricamente, por lo regular no es tan sencillo como oprimir el botón resolver y listo, hay que tener una idea clara del problema que estamos resolviendo, qué nos interesa del problema, y sobre todo, que tipo de algoritmos existen.

Supongamos que ingenuamente, simplemente le damos a resolver:

sol_CR_ingenuo = solve(prob_CR)

Muy bien, ahora grafiquemos lo que obtuvimos haciendo:

ingenuo = plot(sol_CR_ingenuo)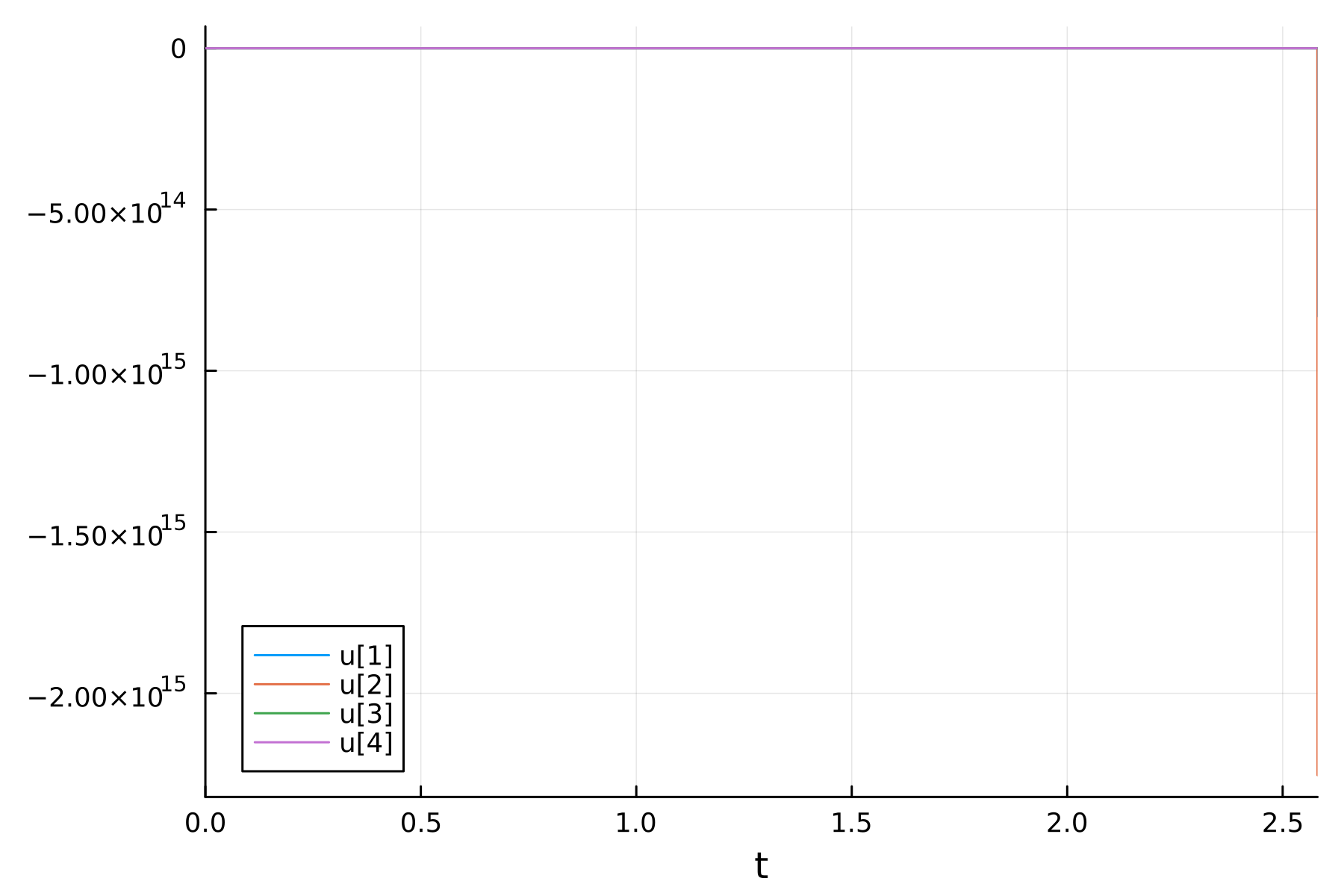

Nuestra gráfica no tiene ningun sentido. Entonces, lo que está pasando es que nos estamos enfrentando a un sistema de ecuaciones diferenciales del tipo stiff o rígidas en español. Este tipo de ecuaciones diferenciales son todo un mundo, sobre el cual pueden saber más aquí, aquí y aquí. Entre muchos más lados.

Pero en esencia lo que está pasando es que los algoritmos tradicionales no funcionan correctamente.

Lo que podemos hacer es ir al siguiente enlace, y buscar algún algoritmo especializado para este tipo de ecuaciones.

Aquí usaremos el algoritmo KenCarp47(), este es un método ESDIRK (Explicit Singly Diagonally Implicit Runge Kutta), de siete etapas de cuarto orden. Este método es parte de una familia de algoritmos que están diseñados para manejar ecuaciones diferenciales rígidas. Aumentaremos el número máximo de iteraciones sólo por si las moscas.

Entonces hagamos:

prob_CR = SecondOrderODEProblem(cuerpo_rigido, du0, u0, tspan, params)

ODEProblem with uType RecursiveArrayTools.ArrayPartition{Float64, Tuple{Vector{Float64}, Vector{Float64}}} and tType Float64. In-place: true
timespan: (0.0, 10.0)
u0: ([0.0, 0.0], [0.0, 0.0])

sol_CR= solve(prob_CR, KenCarp47(), maxiters=1e7)
sol_CR[1:5]

retcode: Success
Interpolation: 3rd order Hermite
t: 5-element Vector{Float64}:
 0.0
 2.4999999999999998e-5
 0.00027499999999999996
 0.0027749999999999993
 0.0043374999999999985
u: 5-element Vector{RecursiveArrayTools.ArrayPartition{Float64, Tuple{Vector{Float64}, Vector{Float64}}}}:
 ([0.0, 0.0], [0.0, 0.0])
 ([0.00032685999214312615, -0.0004902899874999309], [4.085969522329402e-9, -6.128954279218507e-9])
 ([0.0035968144933999965, -0.0053952207395484945], [4.945460046962802e-7, -7.418189382655796e-7])
 ([0.036294755093382966, -0.05444110440780338], [5.035995617645005e-5, -7.553922093387915e-5])
 ([0.056724601745096526, -0.0850829759189515], [0.0001230322224232393, -0.00018454407565608402])

Y además, para comparar, podemos hacer la comparación con lo que sería el sistema aproximado, es decir, haciendo:

$\sin{x} = x$

y

$\cos{x} = 1$

Por lo que nuestro sistema aproximado nos quedaría:

function cuerpo_rigido_aproxx(ddu, du, u, p, t)
    g, l, Ω = p


    ddu[1] = (g * cos(t * Ω) / 3) + (u[2] * du[2]^2 / 2) - (ddu[2] / 2)
    ddu[2] = -3/2 * (g * u[2] + ddu[1]) 
end

cuerpo_rigido_aproxx (generic function with 1 method)

Y resolviendo con las mismas condiciones, tendríamos:

prob_CR_aproxx = SecondOrderODEProblem(cuerpo_rigido_aproxx, du0, u0, tspan, params)

ODEProblem with uType RecursiveArrayTools.ArrayPartition{Float64, Tuple{Vector{Float64}, Vector{Float64}}} and tType Float64. In-place: true
timespan: (0.0, 10.0)
u0: ([0.0, 0.0], [0.0, 0.0])

sol_CR_aproxx = solve(prob_CR_aproxx, KenCarp47(), maxiters=1e7)
sol_CR_aproxx[1:5]

Ahora, graficando en primer lugar la posición del punto, tanto la solución numérica como la solución aproximada tendríamos:

plot(sol_m, idxs = (0, 2), color=:black, label="Numérico", dpi=500)
plot!(sol_m_aprox, idxs = (0, 2), linestyle=:dash, label="Aproximación", ylabel="Posición del punto", ylims=(-7,7), color=:red, title="Posición del punto en cuerpo rígido")

Y obtenemos:

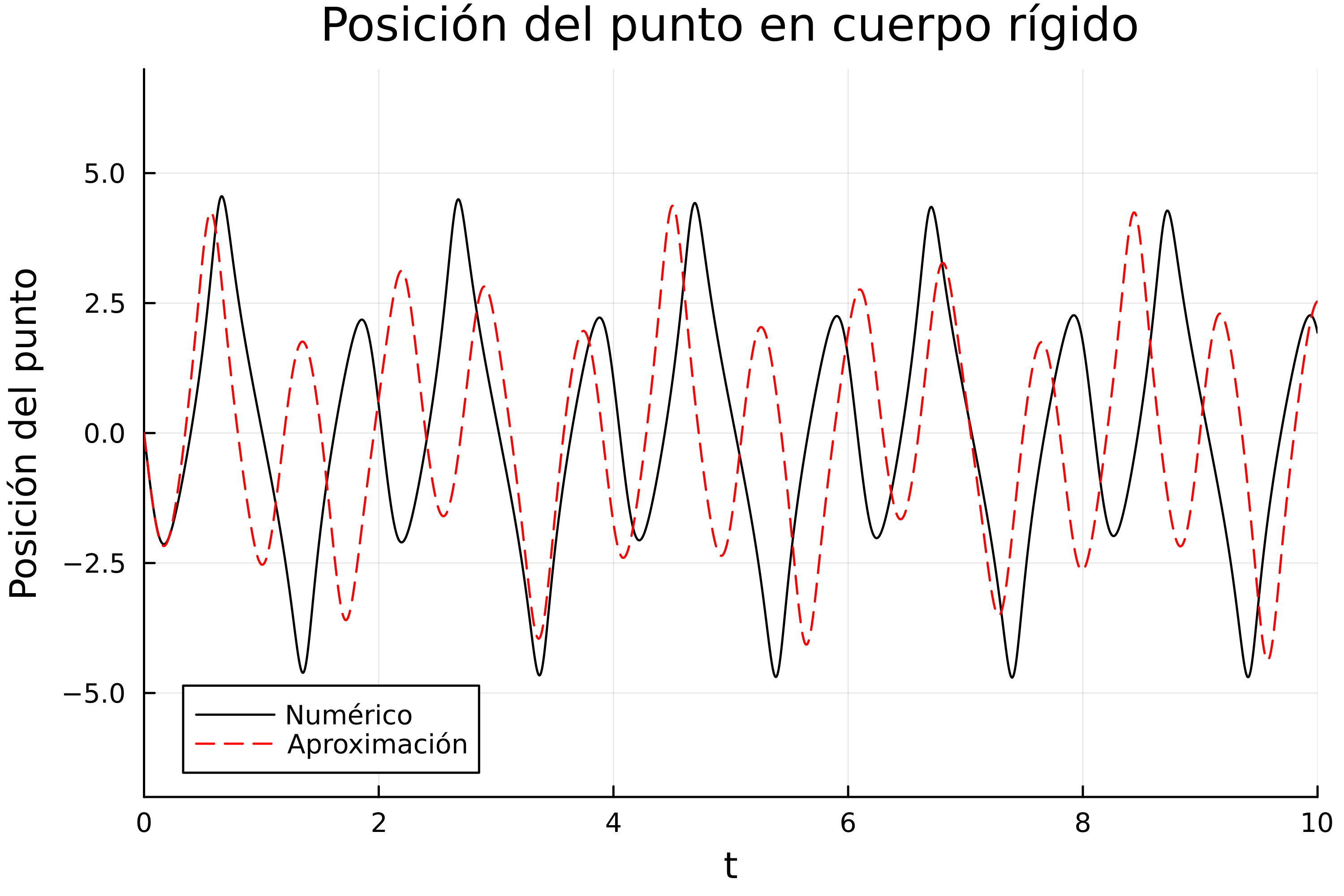
De la misma forma podemos graficar los demás resultados. El índice 0 es el tiempo, el 1 la velocidad del punto, el 2 es la posición del punto como se hizo para graficar el resultado anterior, el índice 3 es la velocidad del ángulo, y el índice 4 es el valor del ángulo, entonces tendríamos:

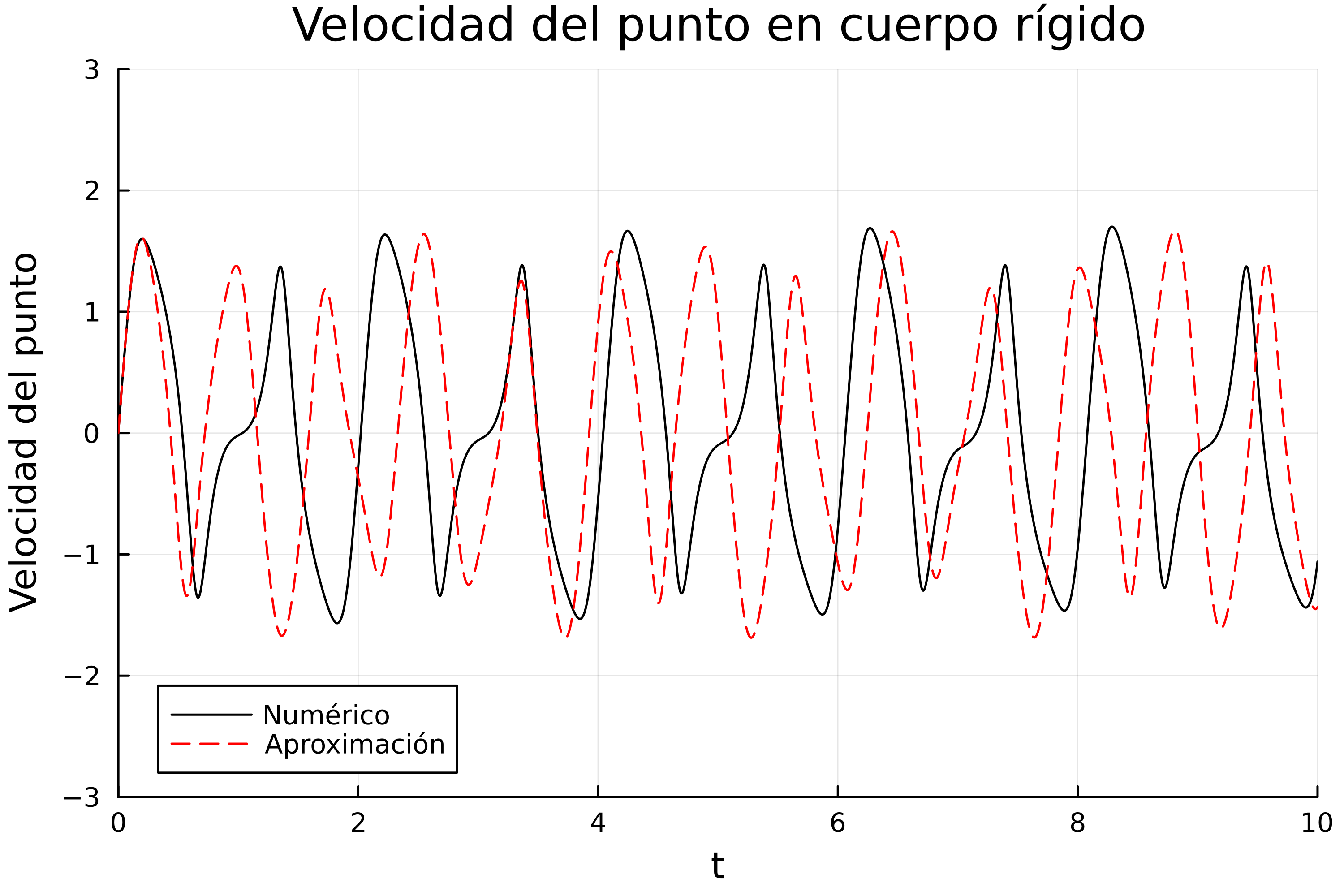
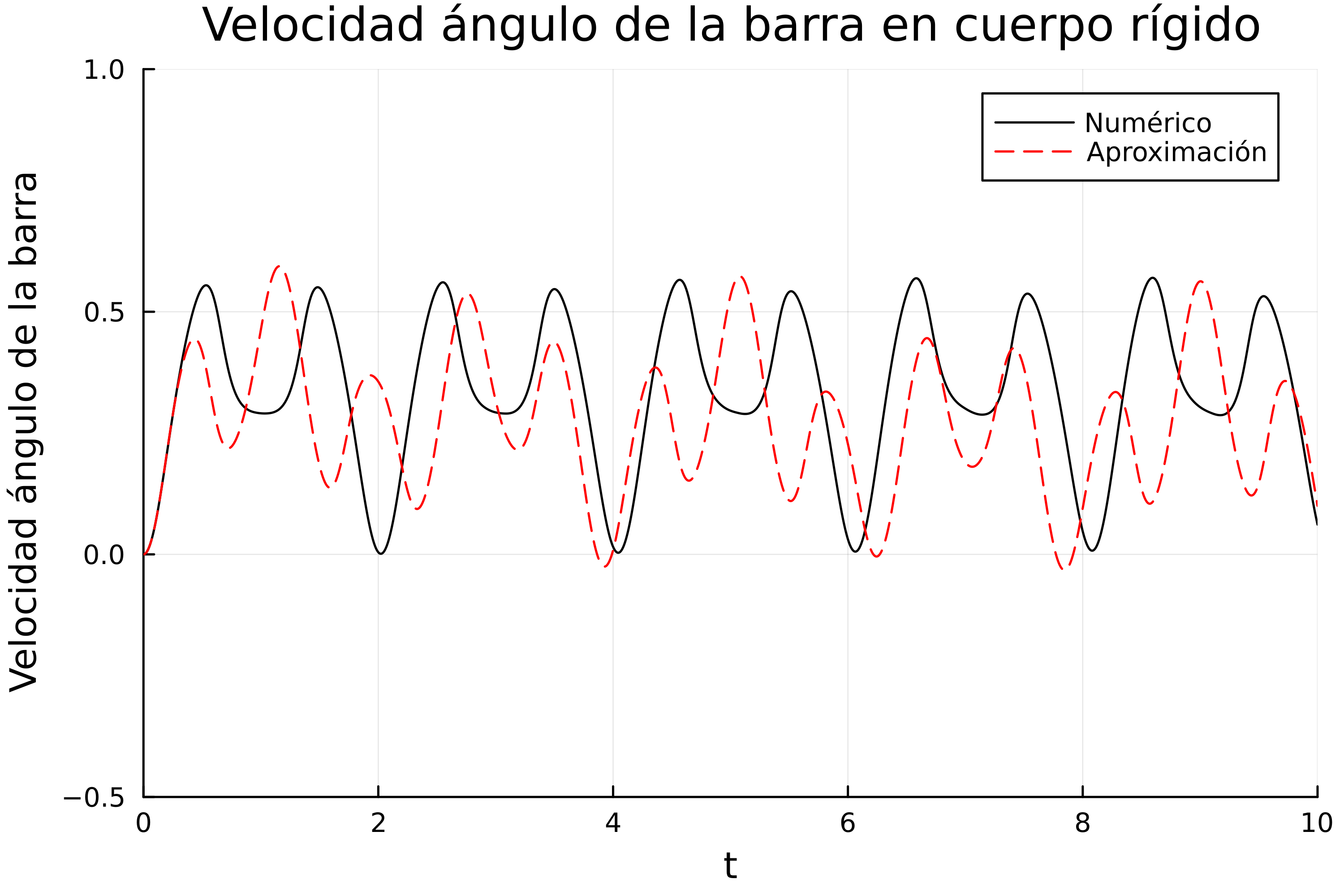
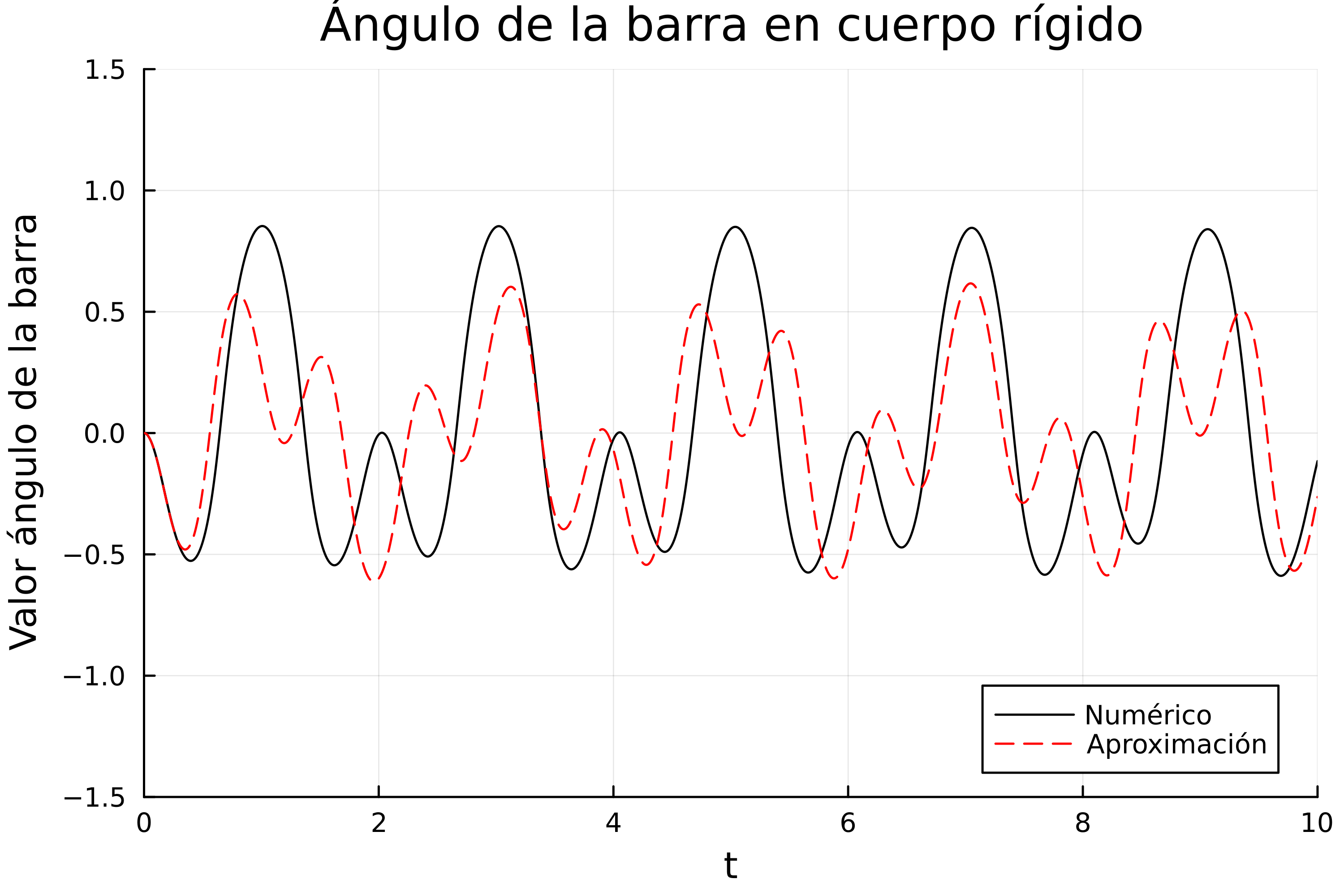
Y como podemos observar, obtenemos movimientos oscilatorios, y también, como era de esperarse, las solución numérica y la aproximada se parecen demasiado recién comienza el sistema.

¿Por qué todo lo que está arriba está mal?

Bueno, casi todo...